矩阵乘法与矩阵快速幂

1 矩阵乘法

1.定义

若矩阵A的大小为\(n \times m\)，矩阵B的大小为\(m \times p\)，则两个矩阵可以做乘法，得到的矩阵C的大小为\(n \times p\)。

\[A = \begin{bmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \end{bmatrix} \]

\[B = \begin{bmatrix} b_{11} & b_{12} \\ b_{21} & b_{22} \\ b_{31} & b_{32} \end{bmatrix} \]

\[C = A \times B = \begin{bmatrix} a_{11}\times b_{11}+ a_{12} \times b_{21}+a_{13} \times b_{31} & a_{11} \times b_{12} + a_{12} \times b_{22} + a_{13} \times b_{32} \\ a_{21} \times b_{11} + a_{22} \times b_{21} + a_{23} \times b_{31} & a_{21} \times b_{12} + a_{22} \times b_{22} + a_{23} \times b_{32} \end{bmatrix} \]

注意：只有矩阵A的列数等于矩阵B的行数时，两个矩阵才能相乘。

2.代码实现

#include<bits/stdc++.h>
#define rg register
#define qwq 0
using namespace std;
const int N = 105;
int n, m, p, a[N][N], b[N][N], c[N][N];
int main() {ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin >> n >> m >> p;for (rg int i = 1; i <= n; i++) {for (rg int j = 1; j <= m; j++) {cin >> a[i][j];}}for (rg int i = 1; i <= m; i++) {for (rg int j = 1; j <= p; j++) {cin >> b[i][j];}}for (rg int i = 1; i <= n; i++) {for (rg int j = 1; j <= p; j++) {for (rg int k = 1; k <= m; k++) {c[i][j] += a[i][k] * b[k][j];}}}for (rg int i = 1; i <= n; i++) {for (rg int j = 1; j <= p; j++) {cout << c[i][j] << " ";}cout << "\n";}return qwq;
}

2 矩阵快速幂

模版

#define mr matrix
struct mr {int m[2][2];
} ans, base;
mr multi(mr a, mr b, int n) {mr tmp;for (rg int i = 0; i < n; i++) {for (rg int j = 0; j < n; j++) {tmp.m[i][j] = 0;for (rg int k = 0; k < n; k++) {tmp.m[i][j] = (tmp.m[i][j] + a.m[i][k] * b.m[k][j]) % mod;}}}return tmp;
}
inline void init() {  //初始化矩阵 base.m[0][0] = base.m[0][1] = base.m[1][0] = 1;base.m[1][1] = 0;ans.m[0][0] = ans.m[1][1] = 1;ans.m[0][1] = ans.m[1][0] = 0;
}
inline int qmod(int k) {  //求矩阵 base的 k次幂init();while (k) {if (k & 1) ans = multi(ans, base, 2);base = multi(base, base, 2);k >>= 1;}return ans.m[0][1];
}

例题1：Fibonacci第n项

题目描述：计算斐波那契数列第n项的后m位。

解析：

斐波那契数列的递推方程试可以写成矩阵的形式：

\[\begin{bmatrix} f[n] \\ f[n-1] \end{bmatrix} = \begin{bmatrix} 1 & 1 \\ 1 & 0 \end{bmatrix} \times \begin{bmatrix} f[n-1] \\ f[n-2] \end{bmatrix} \]

那么：

\[\begin{bmatrix} f[n] \\ f[n-1] \end{bmatrix} = \begin{bmatrix} 1 & 1 \\ 1 & 0 \end{bmatrix} \times \begin{bmatrix} f[n-1] \\ f[n-2] \end{bmatrix} = \begin{bmatrix} 1&1\\1&0 \end{bmatrix} \times \begin{bmatrix} 1&1\\1&0 \end{bmatrix} \times \begin{bmatrix} f[n-2]\\f[n-3] \end{bmatrix} = \begin{bmatrix} 1&1\\1&0 \end{bmatrix}^{n-1} \times \begin{bmatrix} f[1]\\f[0] \end{bmatrix} \]

于是，我们只需要类比普通的快速幂计算矩阵

\[\begin{bmatrix} 1&1\\1&0 \end{bmatrix} \]

的快速幂即可。

代码：

#include<bits/stdc++.h>
#define rg register
#define qwq 0
#define mr matrix
#define int long long
using namespace std;
int n, m;
struct mr {int m[2][2];  //由矩阵的大小决定
} ans, base;
mr multi(mr a, mr b, int n) {mr tmp;for (rg int i = 0; i < n; i++) {for (rg int j = 0; j < n; j++) {tmp.m[i][j] = 0;for (rg int k = 0; k < n; k++) {tmp.m[i][j] = (tmp.m[i][j] + a.m[i][k] * b.m[k][j]) % m;}}}return tmp;
}
inline void init() {  //初始化矩阵 base.m[0][0] = base.m[0][1] = base.m[1][0] = 1;base.m[1][1] = 0;ans.m[0][0] = ans.m[1][1] = 1;ans.m[0][1] = ans.m[1][0] = 0;
}
inline int qmod(int k) {  //求矩阵 base的 k次幂init();while (k) {if (k & 1) ans = multi(ans, base, 2);base = multi(base, base, 2);k >>= 1;}return ans.m[0][1];
}
signed main() {ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin >> n >> m;cout << qmod(n) % m << "\n";return qwq;
}

例题2：Fibonacci前n项和

题目描述：

求\(d_n\)的前n项和\(S_n \bmod m\)。

解析：

考虑递推关系式：\(s[n] = s[n-1]+f[n]\)，写成矩阵形式：

\[\begin{bmatrix} s[n]\\f[n+1]\\f[n] \end{bmatrix} = \begin{bmatrix} 1&1&0\\0&1&1\\0&1&0 \end{bmatrix} \times \begin{bmatrix} s[n-1]\\f[n]\\f[n-1] \end{bmatrix} \]

所以：

\[\begin{bmatrix} s[n]\\f[n+1]\\f[n] \end{bmatrix} = \begin{bmatrix} 1&1&0\\0&1&1\\0&1&0 \end{bmatrix}^{n-1} \times \begin{bmatrix} s[1]\\f[2]\\f[1] \end{bmatrix} \]

例题3：佳佳的Fibonacci

题目描述：

\(T(n) = f_1+2f_2+3f_3+\cdots+nf_n\)，求\(T(n) \bmod m\)。

解析：

递推关系式的矩阵中不能出现变量n，所以要先对递推关系式变形成我们可以处理的情况。

\[\begin{aligned} T_n &= f_1+2f_2+3f_3+\cdots+nf_n \\ &= n \times S_n - S_{n-1} - S_{n-2} - S_{n-3} - \cdots - S_1 \\ &= n \times S_n - \sum _ {i=1}^{n-1} S_i \end{aligned} \]

而

\[\begin{aligned} \sum_{i=1}^{n-1} S_i &= S_1+S_2+S_3+\cdots+S_{n-1} \\ &= f_1+(f_1+f_2)+\cdots+(f_1+f_2+f_3+\cdots+f_{n-1}) \\ &= (n-1)f_1+(n-2)f_2+(n-3)f_3+\cdots+f_n \end{aligned} \]

令\(P_n = \sum_{i=1}^{n-1}S_i\)，则：
\(T_n=n\times S_n-P_n\)

我们不需要递推\(T_n\)，只需要递推\(P_n\)和\(S_n\)，再直接计算得到\(T_n\)。

因为\(P_n=P_{n-1}+S_{n-1}\)，所以：

\[\begin{bmatrix} P_n\\S_n\\f_{n+1}\\f_n \end{bmatrix} = \begin{bmatrix} 1&1&0&0\\0&1&1&0\\0&0&1&1\\0&0&1&0 \end{bmatrix} \times \begin{bmatrix} P_{n-1}\\S_{n-1}\\f_n\\f_{n-1} \end{bmatrix} \]

代码：

#include<bits/stdc++.h>
#define rg register
#define qwq 0
#define mr matrix
using namespace std;
typedef long long ll;
const int N = 100010;
ll mod, n;
struct mr {ll m[5][5];mr() { memset(m, 0, sizeof(m)); }
} a, b;
mr multi(mr x, mr y) {mr ans;for (rg int i = 0; i < 4; i++) {for (rg int j = 0; j < 4; j++) {for (rg int k = 0; k < 4; k++) {ans.m[i][j] = (ans.m[i][j] + x.m[i][k] * y.m[k][j]) % mod;}}}return ans;
}
inline void init() {a.m[0][0] = a.m[0][1] = a.m[1][1] = a.m[1][2] = a.m[2][2] = a.m[2][3] = a.m[3][2] = 1;b.m[1][0] = b.m[2][0] = b.m[3][0] = 1;
}
mr qmod(ll p) {mr ans, base = a;ans.m[0][0] = ans.m[1][1] = ans.m[2][2] = ans.m[3][3] = 1;while (p) {if (p & 1) ans = multi(ans, base);base = multi(base, base);p >>= 1;}return ans;
}
signed main() {ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin >> n >> mod;init();a = qmod(n - 1);mr ans = multi(a, b);cout << (n * ans.m[1][0] - ans.m[0][0] + mod) % mod << "\n";return qwq;
}

递推中存在常数的处理

1.\(f(n) = a \times f(n - 1) + b \times f(n - 2) + c\)

\[\begin{bmatrix} f_n\\f_{n-1}\\c \end{bmatrix} = \begin{bmatrix} a&b&1\\1&0&0\\0&0&1 \end{bmatrix} \times \begin{bmatrix} f_{n-1}\\f_{n-2}\\c \end{bmatrix} \]

2.\(f(n) = c^n - f(n - 1)\)

\[\begin{bmatrix} f_n\\c^n \end{bmatrix} = \begin{bmatrix} -1&c\\0&c \end{bmatrix} \times \begin{bmatrix} f_{n-1}\\c^{n-1} \end{bmatrix} \]

例题4：矩阵幂求和

题目描述：

给定一个矩阵，求\(S = A + A^2 + A^3 + \cdots + A^k\)，求S中的每个数对P取模的结果。

解析：

法一：递归

对式子进行变形，比如：\(A + A^1 + A^2 + A^3 + A^4 + A^5 + A^6\)可以变形为\(A+A^1+A^2+A^3+A^3 \times (A+A^2+A^3) = (A^3+1)(A+A^2+A^3)\)，所以这个式子可以递归。如果k为偶数直接递归即可；如果k为奇数，递归计算\(A^{k-1}\)，之后单独计算\(A^k\)。

#include<bits/stdc++.h>
#define rg register
#define qwq 0
using namespace std;
struct matrix {int n, a[35][35];
} bs, dw;  //dw是单位阵 
int n, k, p;
matrix operator *(matrix x, matrix y) {matrix ans;memset(ans.a, 0, sizeof(ans.a));for (rg int i = 1; i <= n; i++) {for (rg int j = 1; j <= n; j++) {for (rg int k = 1; k <= n; k++) {ans.a[i][j] = (ans.a[i][j] + x.a[i][k] * y.a[k][j]) % p;}}}return ans;
}
inline matrix ksm(int x) {  //求 A^x matrix ans = dw;  //初始dw是斜对角线为 1的矩阵matrix bbs = bs;while (x) {if (x & 1) ans = ans * bbs;bbs = bbs * bbs;x >>= 1;}return ans;
}
inline matrix add(matrix x, matrix y) {matrix ans;memset(ans.a, 0, sizeof(ans.a));for (rg int i = 1; i <= n; i++) {for (rg int j = 1; j <= n; j++) {ans.a[i][j] = (x.a[i][j] + y.a[i][j]) % p;}}return ans;
}
inline matrix dfs(int siz) {  //求 A+A^2+A^3+...+A^siz if (siz == 1) return bs;if (siz & 1) return add(add(ksm(siz / 2), dw) * dfs(siz / 2), ksm(siz));else return add(ksm(siz / 2), dw) * dfs(siz / 2); 
}
int main() {ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin >> n >> k >> p;for (rg int i = 1; i <= n; i++) {for (rg int j = 1; j <= n; j++) {if (i == j) dw.a[i][j] = 1;  //任何矩阵乘对角线为 1的矩阵都是本身 }}for (rg int i = 1; i <= n; i++) {for (rg int j = 1; j <= n; j++) {rg int x;cin >> x;bs.a[i][j] = x;}}matrix ans;ans = dfs(k);for (rg int i = 1; i <= n; i++) {for (rg int j = 1; j <= n; j++) {cout << ans.a[i][j] << " ";}cout << "\n";}return qwq;
}

法二：分块矩阵

我们尝试使用

\[\begin{bmatrix} S_k\\A^k \end{bmatrix} \]

和

\[\begin{bmatrix} S_{k-1}\\A^{k-1} \end{bmatrix} \]

建立关系：

\[\begin{bmatrix} S_k\\S^k \end{bmatrix} = \begin{bmatrix} 1&A\\0&A \end{bmatrix} \times \begin{bmatrix} S_{k-1}\\A^{k-1} \end{bmatrix}\]

我们会发现，这里面是矩阵包含着矩阵，所以这个矩阵的长度为A的长度乘2，同时下面的1也为单位矩阵，0也是一个矩阵，长度都为A的长度。我们求新矩阵的n-1次方，就可以得到\(S_k\)。

#include<bits/stdc++.h>
#define rg register
#define qwq 0
using namespace std;
struct matrix {int n, a[65][65];
} bs;
int n, k, p;
matrix operator *(matrix x, matrix y) {matrix ans;memset(ans.a, 0, sizeof(ans.a));for (rg int i = 1; i <= (n << 1); i++) {for (rg int j = 1; j <= (n << 1); j++) {for (rg int k = 1; k <= (n << 1); k++) {ans.a[i][j] = (ans.a[i][j] + x.a[i][k] * y.a[k][j] % p) % p;}}}return ans;
}
inline matrix ksm(int x) {matrix ans;memset(ans.a, 0, sizeof(ans.a));for (rg int i = 1; i <= (n << 1); i++) {for (rg int j = 1; j <= (n << 1); j++) {if (i == j) ans.a[i][j] = 1;}}matrix bbs;memset(bbs.a, 0, sizeof(bbs.a));for (rg int i = 1; i <= n; i++) {for (rg int j = 1; j <= (n << 1); j++) {bbs.a[i][j] = bs.a[i][j];}}for (rg int i = n + 1; i <= (n << 1); i++) {for (rg int j = 1; j <= n; j++) {bbs.a[i][j] = 0;}}for (rg int i = n + 1; i <= (n << 1); i++) {for (rg int j = n + 1; j <= (n << 1); j++) {if (i == j) bbs.a[i][j] = 1;} }while (x) {if (x & 1) ans = ans * bbs;bbs = bbs * bbs;x >>= 1;}return ans;
}
int main() {ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin >> n >> k >> p;for (rg int i = 1; i <= n; i++) {for (rg int j = 1; j <= n; j++) {rg int x;cin >> x;bs.a[i][j] = x % p;}}for (rg int i = 1; i <= n; i++) {for (rg int j = n + 1; j <= (n << 1); j++) {bs.a[i][j] = bs.a[i][j - n];}}matrix ans = ksm(k - 1);matrix ret;memset(ret.a, 0, sizeof(ret.a));for (rg int i = 1; i <= n; i++) {for (rg int j = 1; j <= (n << 1); j++) {for (rg int k = 1; k <= (n << 1); k++) {ret.a[i][j] = (ret.a[i][j] + bs.a[i][k] * ans.a[k][j] % p) % p;}}}for (rg int i = 1; i <= n; i++) {for (rg int j = n + 1; j <= (n << 1); j++) {cout << ret.a[i][j] << " ";}cout << "\n";}return qwq;
}

例题5：图上路径方案

题目描述：

给定一个有向图的邻接矩阵S，问从点a恰好走K步（允许重复经过边）到达b点的方案数模10007的值。

解析：

如下图：

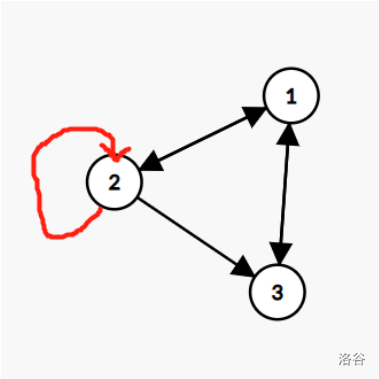
在图的邻接矩阵中，两点之间有连边用1表示，没有用0表示。

\[\begin{bmatrix} 0&1&1\\1&1&1\\1&0&0 \end{bmatrix} \]

换个角度来想，在邻接矩阵A中，\(a_{ij}\)正好表示从点i到点j走一步的方案数，我们尝试将矩阵乘起来，变成\(A^2\)。
在\(A^2\)中，\(A_{11}^2 = a_{11} \times a_{11} + a_{12} \times a_{21} + a_{13} \times a_{31}\)。在这个式子中，\(a_{ik}\)和\(a_{kj}\)都为1，才能对最终的答案贡献1，所以\(A_{ij}^s = A_{ik}^{s-1} + a_{kj}\)表示i到j走s步，可以是i到k走s-1步的基础上再走kj这条边，也就是多走了1步，所以乘一次邻接矩阵，相当于多走一步。所以本题我们直接对邻接矩阵做一个k的快速幂即可。

#include<bits/stdc++.h>
#define rg register
#define qwq 0
using namespace std;
const int mod = 10007;
int n, x, y, k;
struct matrix {int a[35][35];
} base;
matrix operator *(matrix x, matrix y) {matrix p;memset(p.a, 0, sizeof(p.a));for (rg int i = 1; i <= n; i++) {for (rg int j = 1; j <= n; j++) {for (rg int k = 1; k <= n; k++) {p.a[i][j] += (x.a[i][k] * y.a[k][j]) % mod;p.a[i][j] %= mod;}}}return p;
}
matrix ksm(int x) {matrix ans;memset(ans.a, 0, sizeof(ans.a));for (rg int i = 1; i <= n; i++) {for (rg int j = 1; j <= n; j++) {if (i == j) ans.a[i][j] = 1;}}while (x) {if (x & 1) ans = ans * base;base = base * base;x >>= 1;}return ans;
}
signed main() {ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin >> n >> x >> y >> k;for (rg int i = 1; i <= n; i++) {for (rg int j = 1; j <= n; j++) {rg int x;cin >> x;base.a[i][j] = x % mod;}}matrix ans = ksm(k);cout << ans.a[x][y] << "\n";return qwq;
}

例题6：Coww Relays G

题目描述：

给定一张T条边的无向连通图，求S到E经过M条边的最短路。

解析：

我们可以通过动态规划来解决此题。令\(f[i][j]\)表示达到i经过j条边的最短距离，那么转移方程如下：

\(f[i][j] = min(f[k][j - 1] + G[k][i])(1 <= k <= N)\)

其中N为总的点数，如果k和i之间有边相连，则\(G[k][i]\)为边权，否则为正无穷。

上述dp方程时间复杂度为\(O(N^2M)\)，显然会T。
回顾矩阵乘法在图论里的应用式子：

\(C[i][j] = \sum_{k=1}^p A[i][k] \times B[k][j]\)

由于矩阵乘法满足分配律和结合律（不满足交换律），所以我们可以通过矩阵快速幂的方法来加速。于是：

\(C[i][j] = min(A[i][k] + B[k][j])(1<=k<=p)\)

#include<bits/stdc++.h>
#define rg register
#define qwq 0
using namespace std;
struct matrix {int a[205][205];
} bs;
int num[1005], tot;
int n, t, s, e, mx;
matrix operator *(matrix x, matrix y) {matrix c;memset(c.a, 0x3f, sizeof(c.a));for (rg int i = 1; i <= tot; i++) {for (rg int j = 1; j <= tot; j++) {for (rg int k = 1; k <= tot; k++) {c.a[i][j] = min(c.a[i][j], x.a[i][k] + y.a[k][j]);}}}return c;
}
matrix ksm(int x) {matrix ans = bs;while (x) {if (x & 1) ans = ans * bs;bs = bs * bs;x >>= 1;}return ans;
}
signed main() {ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin >> n >> t >> s >> e;memset(bs.a, 0x3f, sizeof(bs.a));for (rg int i = 1; i <= t; i++) {rg int a, b, c;cin >> c >> a >> b;if (!num[a]) num[a] = ++tot;if (!num[b]) num[b] = ++tot;bs.a[num[a]][num[b]] = c;bs.a[num[b]][num[a]] = c;}matrix ans = ksm(n - 1);cout << ans.a[num[s]][num[e]] << "\n"; return qwq;
}

例题7：Blocks

题目描述：

有n个blocks，让你用红，蓝，绿，黄四种颜色染上色，求红色和绿色的block都是偶数个的方案有多少个。

解析：

首先，令

\(dp[i][0]\)表示当涂了前i个blocks之后，红色和绿色都是偶数个的方案数。

\(dp[i][1]\)表示当涂了前i个blocks之后，红色和绿色只有一个是偶数个的方案个数。

\(dp[i][2]\)表示当涂了前i个blocks之后，红色和绿色都不是偶数个的方案个数。

得出状态转移方程：

\(dp[i + 1][0] = 2 \times dp[i][0] + dp[i][1]\)

\(dp[i + 1][1] = 2 \times dp[i][0] + 2 \times dp[i][1] + 2 \times dp[i][2]\)

\(dp[i + 1][2] = dp[i][1] + 2 \times dp[i][2]\)

由于n<=1e9所以\(O(n)\)的dp是不行的，需要矩阵快速幂优化。

\[\begin{bmatrix} A(n)\\B(n)\\C(n) \end{bmatrix} = \begin{bmatrix} 2&1&0\\2&2&2\\0&1&2 \end{bmatrix} \times \begin{bmatrix} A(n-1)\\B(n-1)\\C(n-1) \end{bmatrix} \rightarrow \begin{bmatrix} A(n)\\B(n)\\C(n) \end{bmatrix} = \begin{bmatrix} 2&1&0\\2&2&2\\0&1&2 \end{bmatrix}^n \times \begin{bmatrix} A(0)\\B(0)\\C(0) \end{bmatrix} \]

#include<bits/stdc++.h>
#define rg register
#define qwq 0
using namespace std;
const int mod = 10007;
struct matrix {int a[4][4];matrix() { memset(a, 0, sizeof(a)); }
} bs;
matrix operator *(matrix x, matrix y) {matrix ans;for (rg int i = 0; i < 3; i++) {for (rg int j = 0; j < 3; j++) {for (rg int k = 0; k < 3; k++) {ans.a[i][j] = (ans.a[i][j] + x.a[i][k] * y.a[k][j]) % mod;}}}return ans;
}
matrix operator ^(matrix x, int num) {matrix ans;for (rg int i = 0; i < 3; i++) ans.a[i][i] = 1;while (num) {if (num & 1) ans = ans * x;x = x * x;num >>= 1;}return ans;
}
signed main() {ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int n, t;cin >> t;while (t--) {matrix m;cin >> n;m.a[0][0] = 2, m.a[0][1] = 1, m.a[0][2] = 0;m.a[1][0] = 2, m.a[1][1] = 2, m.a[1][2] = 2;m.a[2][0] = 0, m.a[2][1] = 1, m.a[2][2] = 2;m = m ^ n;cout << m.a[0][0] << "\n";}return qwq;
}

例题8：迷路

题目描述：

该有向图有n个结点，从1到n编号。Windy从1出发，必须恰好在t时刻到达n。求有多少种不同的路径，答案对2009取模。

解析：

首先，如果题目中的每一条边只用0和1表示并且用邻接矩阵A来存这张图，那么在矩阵\(A^t\)中，\(A_{ij}^t\)表示由i到j经过t条边的情况总数。
但这道题这么做显然不行，因为我们所有的推论都建立在边权为1的情况上。

虽然我们不能直接使用我们的结论，但最大边权是9，n也不超过10，不算大。所以我们可以采用拆点：把一个点拆成多个点。

先来拆一个边权不超过2的图：

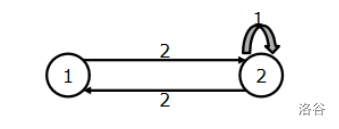
可得矩阵：

\[\begin{bmatrix} 0&2\\2&1 \end{bmatrix} \]

将其拆点：

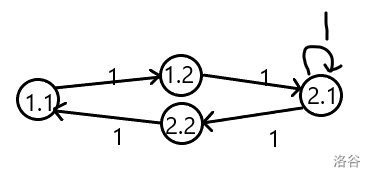
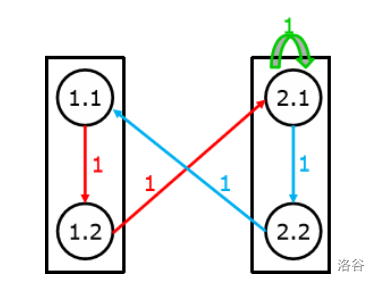
将1.1看成结点1；1.2看成结点2；2.1看成结点3；2.2看成结点4，可得新矩阵：

\[\begin{bmatrix} 0&1&0&0\\0&0&1&0\\0&0&1&1\\1&0&0&0 \end{bmatrix} \]

将其平方：

\[\begin{bmatrix} 0&0&1&0\\0&0&1&1\\1&0&1&1\\0&1&0&0 \end{bmatrix} \]

我们再对非零点进行分类，原先就有的1看成蓝色，后面通过自连得到的1看成红色：

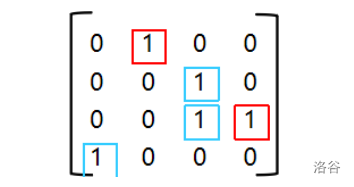
下面的代码可以进行拆点操作：

inline int Cheak(int i, int j) {return (i - 1) * 10 + j;
}
inline void ChaiDian() {for (rg int i = 1; i <= nn; i++) {for (rg int j = 1; j < maxn; j++) {  //maxn表示最大边权 f[Cheak(i, j)][Cheak(i, j + 1)] = 1;  //对红点进行标记 }for (rg int j = 1; j <= nn; j++) {if (a[i][j]) {  //对本来就存在的点进行标记 f[Cheak(i, a[i][j])][Cheak(j, 1)] = 1;}}}
}

最终代码：

#include<bits/stdc++.h>
#define rg register
#define qwq 0
using namespace std;
const int mod = 2009;
int n, nn, t;
struct matrix {int ma[205][205];	void clear() { memset(ma, 0, sizeof(ma)); }
} A;
matrix operator *(matrix x, matrix y) {matrix ans;ans.clear();for (rg int i = 1; i <= n; i++) {for (rg int j = 1; j <= n; j++) {for (rg int k = 1; k <= n; k++) {ans.ma[i][j] = (ans.ma[i][j] + x.ma[i][k] * y.ma[k][j]) % mod;}}}return ans;
}
matrix ksm(matrix x, int b) {matrix ans;ans.clear();for (rg int i = 1; i <= n; i++) {ans.ma[i][i] = 1;}while (b) {if (b & 1) ans = ans * x;x = x * x;b >>= 1;}return ans;
}
inline int Cheak(int i, int j) {return (i - 1) * 10 + j;
}
inline void ChaiDian() {for (rg int i = 1; i <= nn; i++) {for (rg int j = 1; j < 10; j++) {  //maxn表示最大边权 A.ma[Cheak(i, j)][Cheak(i, j + 1)] = 1;  //对红点进行标记 }for (rg int j = 1; j <= nn; j++) {rg char xx;rg int x;cin >> xx;x = xx - '0';if (x) {  //对本来就存在的点进行标记 A.ma[Cheak(i, x)][Cheak(j, 1)] = 1;}}}
}
int main() {ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin >> n >> t;nn = n;n *= 10;ChaiDian();A = ksm(A, t);cout << A.ma[1][n - 9] << "\n";return qwq;
}

完结撒花~