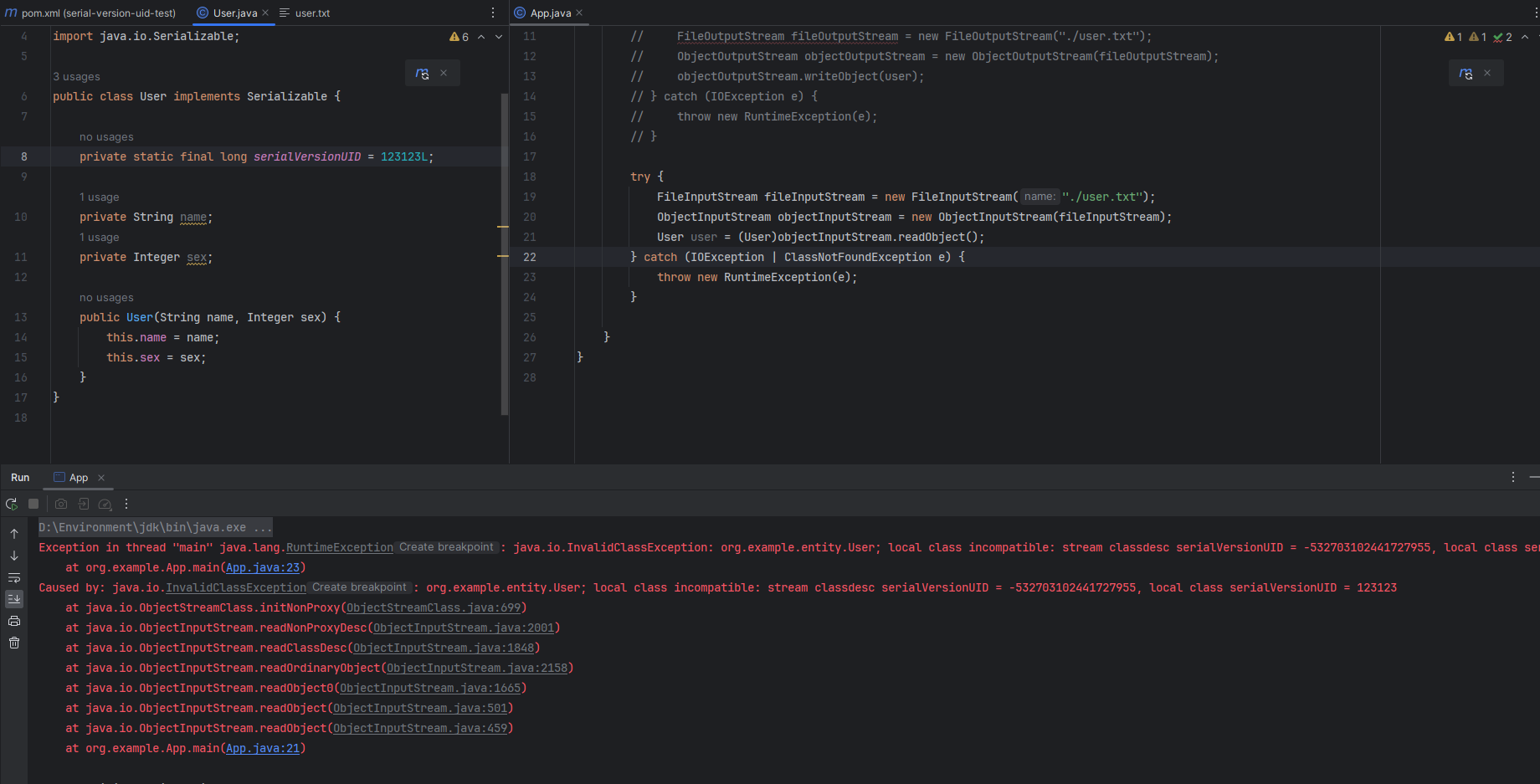
$\quad $ 直接变堂食,考试完不到3分钟我的分数翻倍了(👀)
T1 忘八棋
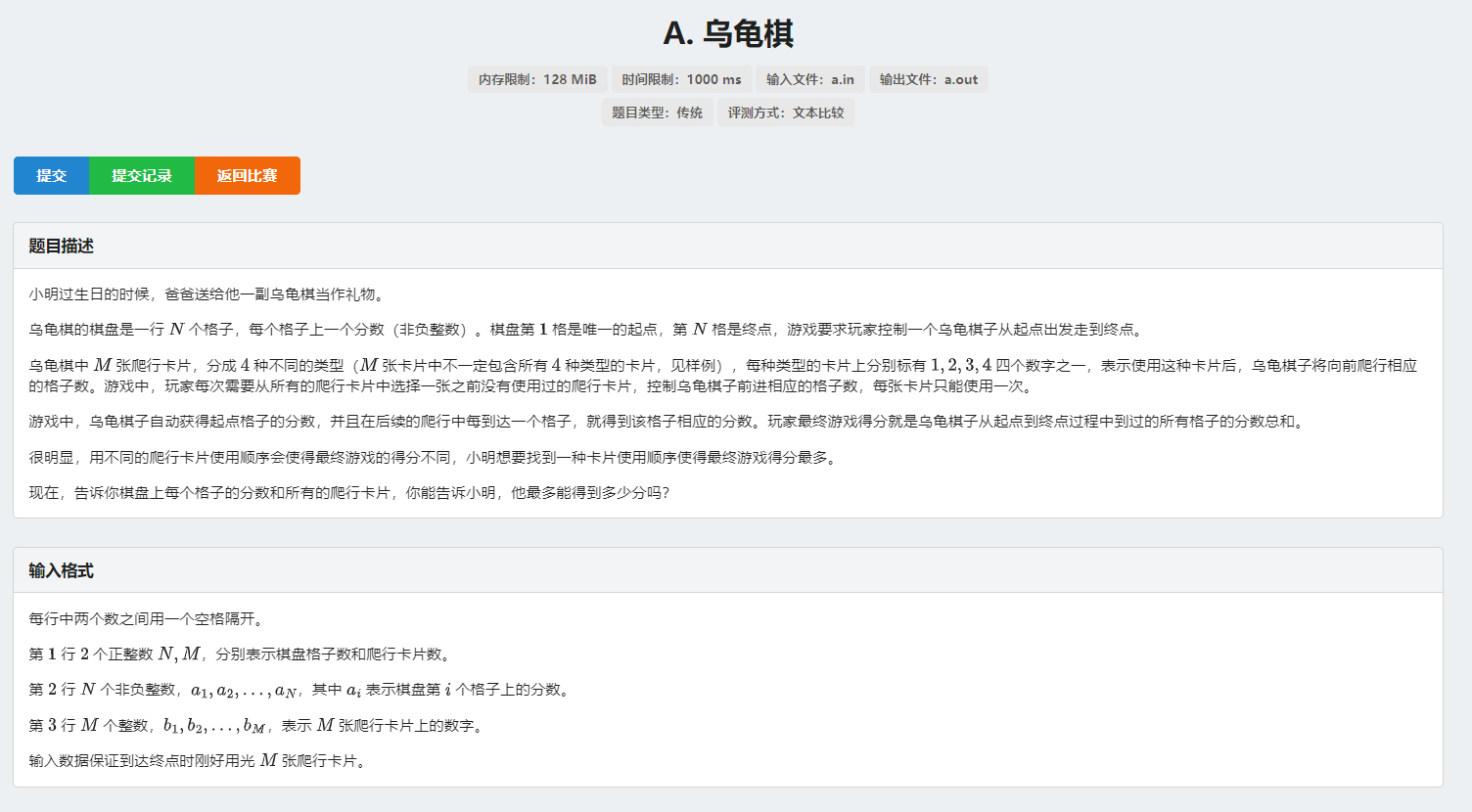
$\quad $ 直接四层循环枚举状态即可,\(O(30^4)\)。开始一眼五层循环,不但 T 了还 WA 了,考完试cpa告诉我枚举的时候位置就确定了,直接变消愁🤡。
点击查看代码
#include<bits/stdc++.h>using namespace std;#define yhl 0#define int long long const int M=350,N=41;int k[M],f[N][N][N][N],n,m;int cnt[10],now=0,x;inline int read(){int ans=0;bool flag=0;char ch=getchar();while(ch<'0'||ch>'9'){if(ch=='-')flag=1;ch=getchar();}while(ch>='0'&&ch<='9')ans=(ans<<3)+(ans<<1)+ch-'0',ch=getchar();return flag?~ans+1:ans;}int get_site(int a,int b,int c,int d){return a+(b<<1)+(c<<1)+c+(d<<2);}signed main(){n=read(),m=read();for(int i=1;i<=n;i=-~i)k[i]=read();for(int i=1;i<=m;i=-~i)cnt[read()]++;for(int a=0;a<=cnt[1];a=-~a){for(int b=0;b<=cnt[2];b=-~b){for(int c=0;c<=cnt[3];c=-~c){for(int d=0;d<=cnt[4];d=-~d){if(a)f[a][b][c][d]=max(f[a][b][c][d],f[a-1][b][c][d]);if(b)f[a][b][c][d]=max(f[a][b][c][d],f[a][b-1][c][d]);if(d)f[a][b][c][d]=max(f[a][b][c][d],f[a][b][c][d-1]);if(c)f[a][b][c][d]=max(f[a][b][c][d],f[a][b][c-1][d]);f[a][b][c][d]+=k[get_site(a,b,c,d)+1];}}}}printf("%lld",f[cnt[1]][cnt[2]][cnt[3]][cnt[4]]);return yhl;}
T2 划分大理石
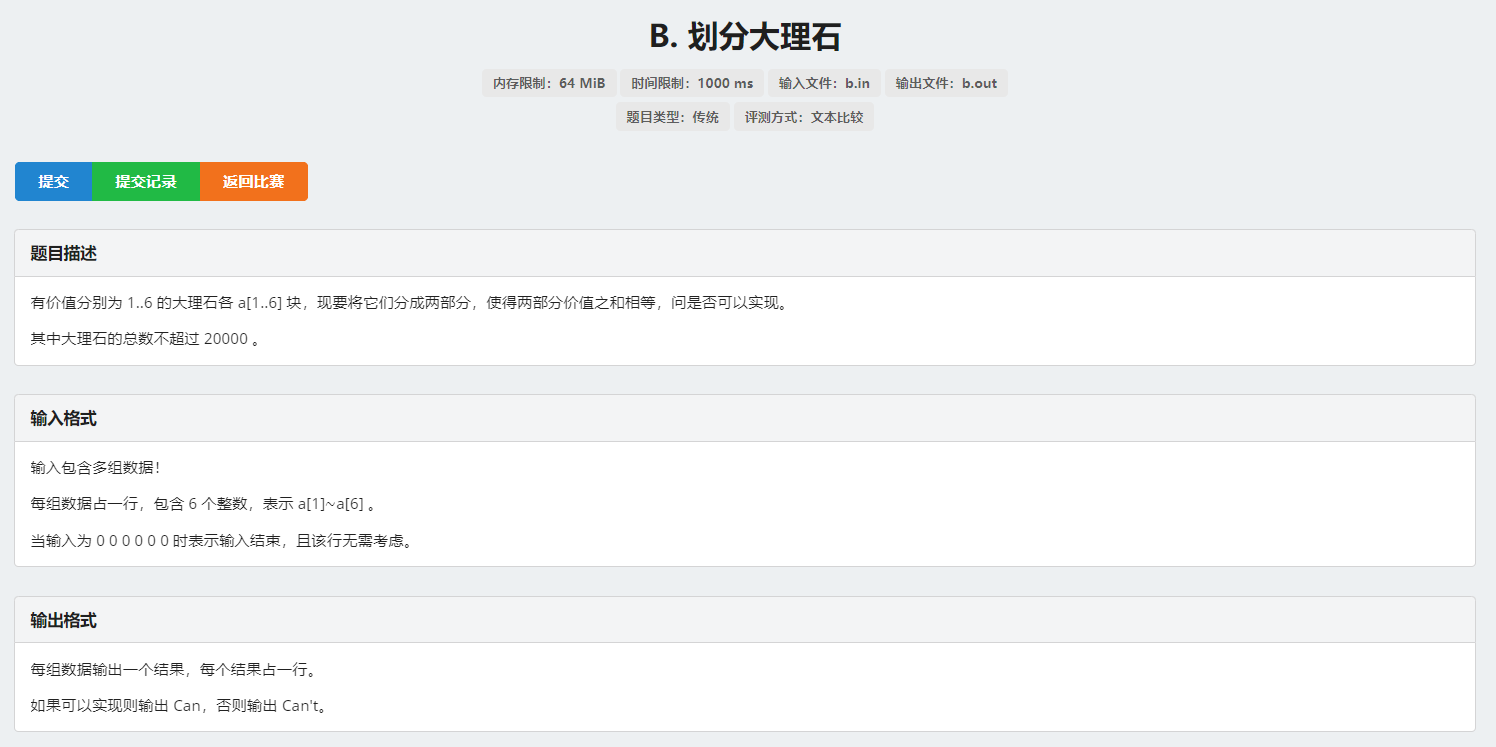
$\quad $ 背包板子题,先判断一下总长度是否为奇数。若是偶数就直接以 $\lfloor \Sigma _{i=1} ^{6}{cnt[i]}/2 \rfloor $ 为背包容量跑一遍背包就行。
点击查看代码
#include<bits/stdc++.h>using namespace std;#define yhl 0const int N=20005;int f[N*6],m,cnt[7],tot,v[N];inline void init(){tot&=0;m&=0;for(int i=1;i<=6;i=-~i){m+=cnt[i]*i;v[++tot]=i;}}int main(){while(scanf("%d%d%d%d%d%d",&cnt[1],&cnt[2],&cnt[3],&cnt[4],&cnt[5],&cnt[6])&&(cnt[1]||cnt[2]||cnt[3]||cnt[4]||cnt[5]||cnt[6])){init();if(m&1)printf("Can't\n");else{m>>=1;for(int i=0;i<=m;i=-~i)f[i]&=0; for(int i=1;i<=tot;i=-~i){for(int j=m;j>=v[i];j--){for(int k=1;k<=min(j/v[i],cnt[i]);k++)f[j]=max(f[j],f[j-k*v[i]]+k*v[i]);}}if(f[m]==m)printf("Can\n");else printf("Can't\n");}}return yhl;}
T3 干草堆

$\quad $ 记 \(f[i]\) 为放置到倒数第 \(i\) 块草时能堆放的最大层数,\(g[i]\) 为此时最下层的最小宽度。则有
\[f[i]=Max{ \{ {f[j]+1} \}} \quad j\in [i+1,n+1] and \Sigma _{k=i} ^{j-1} {w[k]}\leq g(i)
\]
$\quad $ 当该式第一次被满足时取到最优解,后半部分拿前缀和或者后缀和维护即可。
点击查看代码
#include<bits/stdc++.h>using namespace std;#define int long long #define yhl 0const int N=1e5+10;int f[N],g[N],n,w[N],sum[N];inline int read(){int ans=0;bool flag=0;char ch=getchar();while(ch<'0'&&ch>'9'){if(ch=='-')flag=1;ch=getchar();}while(ch>='0'&&ch<='9')ans=(ans<<3)+(ans<<1)+ch-'0',ch=getchar();return flag?(~ans+1):ans;}signed main(){scanf("%lld",&n);for(int i=1;i<=n;i++)scanf("%lld",&w[i]);for(int i=n;i>=1;i--)sum[i]=sum[i+1]+w[i];for(int i=n;i>=1;i--){for(int j=i+1;j<=n+1;j++){if(g[j]<=sum[i]-sum[j]&&f[i]<=f[j]+1){f[i]=f[j]+1;g[i]=sum[i]-sum[j];break;}}}printf("%lld",f[1]);return yhl;}
T4 围栏障碍训练场
$\quad $ 首先是暴力,每次都找到某个端点向下碰到的第一个栅栏(不包含端点),反复转移即可。(但本蒟蒻没打出来)
$\quad $ 对于寻找的过程,可以用线段树进行维护,做到 \(O(log_2n)\) 查询,总时间复杂度 \(O(nlog_2n)\)
点击查看代码
#include<bits/stdc++.h>using namespace std;const int N=50005,X=100000;#define yhl 0#define int long long#define ld (x<<1)#define rd (x<<1|1) int f[N][2],n,S,ans=INT_MAX,l[N],r[N];inline int read(){int ans=0;bool flag=0;char ch=getchar();while(ch<'0'||ch>'9'){if(ch=='-')flag=1;ch=getchar();}while(ch>='0'&&ch<='9')ans=(ans<<3)+(ans<<1)+ch-'0',ch=getchar();return flag?~ans+1:ans;}struct stu{int l,r,m;}s[X<<3];inline int absl(int x){return x<0?(~x+1):x;}void build(int x,int l,int r){s[x].l=l;s[x].r=r;s[x].m=-1;if(l==r){s[x].m=0;return;}int mid=l+r>>1;build(ld,l,mid);build(rd,mid+1,r);}void push_down(int x){if(s[x].l!=s[x].r&&s[x].m!=-1){s[ld].m=s[rd].m=s[x].m;s[x].m=-1;}}void update(int x,int l,int r,int val){if(l<=s[x].l&&s[x].r<=r){s[x].m=val;return;}push_down(x);int mid=s[x].l+s[x].r>>1;if(l<=mid)update(ld,l,r,val);if(r>mid)update(rd,l,r,val);}int query(int x,int pos){if(s[x].l==s[x].r)return s[x].m;push_down(x);int mid=s[x].l+s[x].r>>1;if(pos<=mid)return query(ld,pos);else return query(rd,pos);}signed main(){n=read(),S=read()+X;build(1,0,X*2);l[0]=r[0]=X;for(int i=1;i<=n;i++){l[i]=read()+X,r[i]=read()+X;int j=query(1,l[i]);f[i][0]=min(f[j][0]+absl(l[i]-l[j]),f[j][1]+absl(l[i]-r[j]));j=query(1,r[i]);f[i][1]=min(f[j][0]+absl(r[i]-l[j]),f[j][1]+absl(r[i]-r[j]));update(1,l[i],r[i],i);}printf("%lld",min(f[n][1]+abs(r[n]-S),f[n][0]+abs(l[n]-S)));return yhl;}
$\quad $ 先是暴搜 \(O(2^n)\) ,这只是理论复杂度,实际是小于 \(O(2^n)\) 的。
暴搜
#include<bits/stdc++.h>using namespace std;const int N=30005;#define yhl 0#define int long long int f[N][2],n,s,a[N][2],ans=INT_MAX;inline int read(){int ans=0;bool flag=0;char ch=getchar();while(ch<'0'||ch>'9'){if(ch=='-')flag=1;ch=getchar();}while(ch>='0'&&ch<='9')ans=(ans<<3)+(ans<<1)+ch-'0',ch=getchar();return flag?~ans+1:ans;}void dfs(int ceng,int x,int now){if(ceng>=n){ans=min(ans,now+abs(x));return;}for(int i=ceng+1;i<=n+1;i++){if(i==n+1){ans=min(ans,now+abs(x));return ;}if(x>a[i][0]&&x<a[i][1]){dfs(i,a[i][0],now+x-a[i][0]);dfs(i,a[i][1],now+a[i][1]-x);return ;}}}signed main(){n=read(),s=read();for(int i=1;i<=n;i++)a[i][0]=read(),a[i][1]=read();dfs(1,s,0);printf("%lld",ans);return yhl;}
$To Be Continued $