矩阵基础知识
在具体描述如何构建模型矩阵、观察矩阵和投影矩阵之前,我们在这一节先介绍矩阵的各种基础知识(只介绍需要用到的知识)。
矩阵的基本含义
由\(m \times n\)个数\(a_{ij}(i \in [1, m], j \in [1, n])\)组成的数列被称为m行n列的矩阵\(A\)(一般用大写数字表示矩阵):
\[A_{mn} = \left[
\begin{matrix}
a_{11} & a_{12} & a_{13} & ... & a_{1n} \\
a_{21} & a_{22} & a_{23} & ... & a_{2n} \\... & ... & ... & ... & ... \\
a_{m1} & a_{m2} & a_{m3} & ... & a_{mn} \\
\end{matrix}
\right].
\]
值得注意的是有一些特殊的矩阵:
- 当\(m = n\)时,即矩阵\(A\)的行数和列数相等时被称为方阵。
- 当方阵的所有元素中除了对角元素的其余元素为0时,被称为对角矩阵。
- 当对角矩阵的对角元素都为1时,被称为单位矩阵(\(I\))。
- 当方阵满足\(a_{ij} = a_{ji}\)时,被称为对称矩阵。
矩阵的运算
矩阵与标量的乘法:矩阵中每个元素与标量相乘
\[\alpha \times A_{mn} = \left[
\begin{matrix}
\alpha \times a_{11} & \alpha \times a_{12} & \alpha \times a_{13} & ... & \alpha \times a_{1n} \\
\alpha \times a_{21} & \alpha \times a_{22} & \alpha \times a_{23} & ... & \alpha \times a_{2n} \\... & ... & ... & ... & ... \\
\alpha \times a_{m1} & \alpha \times a_{m2} & \alpha \times a_{m3} & ... & \alpha \times a_{mn} \\
\end{matrix}
\right].
\]
矩阵加法:只有两个矩阵的维度一致时才能进行加法
\[\begin{aligned}
\textcolor{blue}{A_{mn}} + \textcolor{green}{B_{mn}} & = \left[
\textcolor{blue}{
\begin{matrix}
a_{11} & a_{12} & a_{13} & ... & a_{1n} \\
a_{21} & a_{22} & a_{23} & ... & a_{2n} \\... & ... & ... & ... & ... \\
a_{m1} & a_{m2} & a_{m3} & ... & a_{mn} \\
\end{matrix}
}
\right] + \left[
\textcolor{green}{
\begin{matrix}
b_{11} & b_{12} & b_{13} & ... & b_{1n} \\
b_{21} & b_{22} & b_{23} & ... & b_{2n} \\... & ... & ... & ... & ... \\
b_{m1} & b_{m2} & b_{m3} & ... & b_{mn} \\
\end{matrix}
}
\right] \\
& = \left[
\begin{matrix}
\textcolor{blue}{a_{11}} + \textcolor{green}{b_{11}} & \textcolor{blue}{a_{12}} + \textcolor{green}{b_{12}} & \textcolor{blue}{a_{13}} + \textcolor{green}{b_{13}} & ... & \textcolor{blue}{a_{1n}} + \textcolor{green}{b_{1n}} \\
\textcolor{blue}{a_{21}} + \textcolor{green}{b_{21}} & \textcolor{blue}{a_{22}} + \textcolor{green}{b_{22}} & \textcolor{blue}{a_{23}} + \textcolor{green}{b_{23}} & ... & \textcolor{blue}{a_{2n}} + \textcolor{green}{b_{2n}} \\... & ... & ... & ... & ... \\
\textcolor{blue}{a_{m1}} + \textcolor{green}{b_{m1}} & \textcolor{blue}{a_{m2}} + \textcolor{green}{b_{m2}} & \textcolor{blue}{a_{m3}} + \textcolor{green}{b_{m3}} & ... & \textcolor{blue}{a_{mn}} + \textcolor{green}{b_{mn}} \\
\end{matrix}
\right].
\end{aligned}
\]
根据公式也可以推导得到:
- \(A + B = B + A\).
- \(A + B + C = A + (B + C)\).
矩阵减法:可以进行如下简单变换
\[A - B = A + (-1) \times B.
\]
矩阵乘法:矩阵乘法是有顺序的,只有第一个矩阵的列数与第二个矩阵的行数相等时才能进行乘法运算,即\(A_{mn} \times B_{nk} = C_{mk}\)
\[\begin{aligned}
\textcolor{blue}{A_{mn}} \times \textcolor{green}{B_{nk}} & = \left[
\textcolor{blue}{
\begin{matrix}
a_{11} & a_{12} & a_{13} & ... & a_{1n} \\
a_{21} & a_{22} & a_{23} & ... & a_{2n} \\... & ... & ... & ... & ... \\
a_{m1} & a_{m2} & a_{m3} & ... & a_{mn} \\
\end{matrix}
}
\right] \times \left[
\textcolor{green}{
\begin{matrix}
b_{11} & b_{12} & b_{13} & ... & b_{1k} \\
b_{21} & b_{22} & b_{23} & ... & b_{2k} \\... & ... & ... & ... & ... \\
b_{n1} & b_{n2} & b_{n3} & ... & b_{nk} \\
\end{matrix}
}
\right] \\
& = \left[
\begin{matrix}
\sum_{i = 1}^n \textcolor{blue}{a_{1i}} \times \textcolor{green}{b_{i1}} & \sum_{i = 1}^n \textcolor{blue}{a_{1i}} \times \textcolor{green}{b_{i2}} & \sum_{i = 1}^n \textcolor{blue}{a_{1i}} \times \textcolor{green}{b_{i3}} & ... & \sum_{i = 1}^n \textcolor{blue}{a_{1i}} \times \textcolor{green}{b_{ik}} \\
\sum_{i = 1}^n \textcolor{blue}{a_{2i}} \times \textcolor{green}{b_{i1}} & \sum_{i = 1}^n \textcolor{blue}{a_{2i}} \times \textcolor{green}{b_{i2}} & \sum_{i = 1}^n \textcolor{blue}{a_{2i}} \times \textcolor{green}{b_{i3}} & ... & \sum_{i = 1}^n \textcolor{blue}{a_{2i}} \times \textcolor{green}{b_{ik}} \\... & ... & ... & ... & ... \\
\sum_{i = 1}^n \textcolor{blue}{a_{mi}} \times \textcolor{green}{b_{i1}} & \sum_{i = 1}^n \textcolor{blue}{a_{mi}} \times \textcolor{green}{b_{i2}} & \sum_{i = 1}^n \textcolor{blue}{a_{mi}} \times \textcolor{green}{b_{i3}} & ... & \sum_{i = 1}^n \textcolor{blue}{a_{mi}} \times \textcolor{green}{b_{ik}} \\
\end{matrix}
\right].
\end{aligned}
\]
可以发现矩阵的乘法就是\(c_{ij} = \sum_{t = 1}^n a_{it} \times b_{tj}\),即矩阵\(A\)的第\(i\)行组成的行向量与矩阵\(B\)的第\(j\)列组成的列向量进行内积。这也是为什么矩阵相乘要求第一个矩阵的列数等于第二个矩阵的行数。也可以看到矩阵乘法是有顺序的,即\(A \times B \neq B \times A\).
根据公式可以推导出:
- \(A \times B \times C = A \times (B \times C).\)
- \(A \times (B + C) = A \times B + A \times C.\)
- \((A + B) \times C = A \times C + B \times C.\)
- 矩阵乘法不满足交换律!
转置:即将矩阵的翻转
\[A_{mn}' = \left[
\begin{matrix}
a_{11} & a_{12} & a_{13} & ... & a_{1n} \\
a_{21} & a_{22} & a_{23} & ... & a_{2n} \\... & ... & ... & ... & ... \\
a_{m1} & a_{m2} & a_{m3} & ... & a_{mn} \\
\end{matrix}
\right]' = \left[
\begin{matrix}
a_{11} & a_{21} & a_{31} & ... & a_{m1} \\
a_{12} & a_{22} & a_{32} & ... & a_{m2} \\... & ... & ... & ... & ... \\
a_{1n} & a_{2n} & a_{3n} & ... & a_{mn} \\
\end{matrix}
\right].
\]
可以看到一个m行n列的矩阵转置后变成了一个n行m列的矩阵。我们也可以说对称矩阵即其转置等于本身的矩阵:\(A' = A\).
有时候矩阵的转置也写为:\(A^T\).
由公式可以推导:
- \((A \times B)' = A' \times B'.\)
矩阵变换
齐次坐标
假设目前在三维坐标中存在某个顶点\((x, y, z)\),为了方便进行坐标的位移变换,我们额外添加一个维度将其转换为齐次坐标\((x, y, z, 1)\),注意这里虽然是四维坐标,但仍然代表着三维空间中的某个点。
平移变换
现在期望将顶点\((x, y, z)\),平移至新的顶点\((x + a, y + b, z + c)\),那么可以构建如下的变换矩阵:
\[P = \left[
\begin{matrix}
1 & 0 & 0 & a \\
0 & 1 & 0 & b \\
0 & 0 & 1 & c \\
0 & 0 & 0 & 1
\end{matrix}
\right].
\]
此时对于原始顶点的齐次坐标\(\alpha = (x, y, z, 1)\),就可以通过简单的矩阵乘法进行变换(注意矩阵乘法顺序,要左乘变换矩阵):
\[\alpha' = P \times \alpha = \left[
\begin{matrix}
1 & 0 & 0 & a \\
0 & 1 & 0 & b \\
0 & 0 & 1 & c \\
0 & 0 & 0 & 1
\end{matrix}
\right] \times \left[
\begin{matrix}
x \\ y \\ z \\ 1
\end{matrix}
\right] = \left[
\begin{matrix}
x + a \\ y + b \\ z + c \\ 1
\end{matrix}
\right].
\]
我们就得到了新的顶点的齐次坐标\(\alpha' = (x + a, y + b, z + c, 1)\).
缩放变换
现在期望针对顶点\((x, y, z)\)的每一个维度分别进行缩放,分别扩大\(a, b, c\)倍,形成新的顶点即\((a \times x, b \times y, c \times z)\),可以构建如下的变换矩阵:
\[P = \left[
\begin{matrix}
a & 0 & 0 & 0 \\
0 & b & 0 & 0 \\
0 & 0 & c & 0 \\
0 & 0 & 0 & 1
\end{matrix}
\right].
\]
此时对于原始顶点的齐次坐标\(\alpha = (x, y, z, 1)\),就可以通过简单的矩阵乘法进行变换(注意矩阵乘法顺序,要左乘变换矩阵):
\[\alpha' = P \times \alpha = \left[
\begin{matrix}
a & 0 & 0 & 0 \\
0 & b & 0 & 0 \\
0 & 0 & c & 0 \\
0 & 0 & 0 & 1
\end{matrix}
\right] \times \left[
\begin{matrix}
x \\ y \\ z \\ 1
\end{matrix}
\right] = \left[
\begin{matrix}
a \times x \\ b \times y \\ c \times z \\ 1
\end{matrix}
\right].
\]
我们就得到了新的顶点的齐次坐标\(\alpha' = (a \times x, b \times y, c \times z, 1)\).
旋转变换
我们直接考虑三维坐标旋转(相对于原点),由于对每个轴的旋转不一样,我们分别讨论绕x、y和z轴旋转的变换矩阵:
绕x轴逆时针旋转\(\alpha\)

如上图所示,点\(a\)绕x轴逆时针旋转\(\alpha\)变为新的点\(a'\)。不妨设点\(a\)距离原点为\(\rho\),那么原始点\(a\)的坐标如下:
\[\begin{aligned}
x & = x \\
y & = \rho \cos \beta \\
z & = \rho \sin \beta
\end{aligned}
\]
旋转后的点\(a'\)的坐标为:
\[\begin{aligned}
x & = x \\
y & = \rho \cos (\alpha + \beta) = \rho \cos \alpha \cos \beta - \rho \sin \alpha \sin \beta = y \cos \alpha - z \sin \alpha \\
z & = \rho \sin (\alpha + \beta) = \rho \sin \alpha \cos \beta + \rho \cos \alpha \sin \beta = y \sin \alpha + z \cos \alpha
\end{aligned}
\]
因此绕x轴逆时针旋转\(\alpha\)的变换矩阵为:
\[P = \left[
\begin{matrix}
1 & 0 & 0 & 0 \\
0 & \cos \alpha & -\sin \alpha & 0 \\
0 & \sin \alpha & \cos \alpha & 0 \\
0 & 0 & 0 & 1
\end{matrix}
\right].
\]
绕y轴逆时针旋转\(\alpha\)

如上图所示,点\(a\)绕y轴逆时针旋转\(\alpha\)变为新的点\(a'\)。不妨设点\(a\)距离原点为\(\rho\),那么原始点\(a\)的坐标如下:
\[\begin{aligned}
x & = \rho \sin \beta \\
y & = y \\
z & = \rho \cos \beta
\end{aligned}
\]
旋转后的点\(a'\)的坐标为:
\[\begin{aligned}
x & = \rho \sin (\alpha + \beta) = \rho \sin \alpha \cos \beta + \rho \cos \alpha \sin \beta = x \cos \alpha + z \sin \alpha \\
y & = y \\
z & = \rho \cos (\alpha + \beta) = \rho \cos \alpha \cos \beta - \rho \sin \alpha \sin \beta = -x \sin \alpha + z \cos \alpha
\end{aligned}
\]
因此绕y轴逆时针旋转\(\alpha\)的变换矩阵为:
\[P = \left[
\begin{matrix}
\cos \alpha & 0 & \sin \alpha & 0 \\
0 & 1 & 0 & 0 \\
-\sin \alpha & 0 & \cos \alpha & 0 \\
0 & 0 & 0 & 1
\end{matrix}
\right].
\]
绕z轴逆时针旋转\(\alpha\)
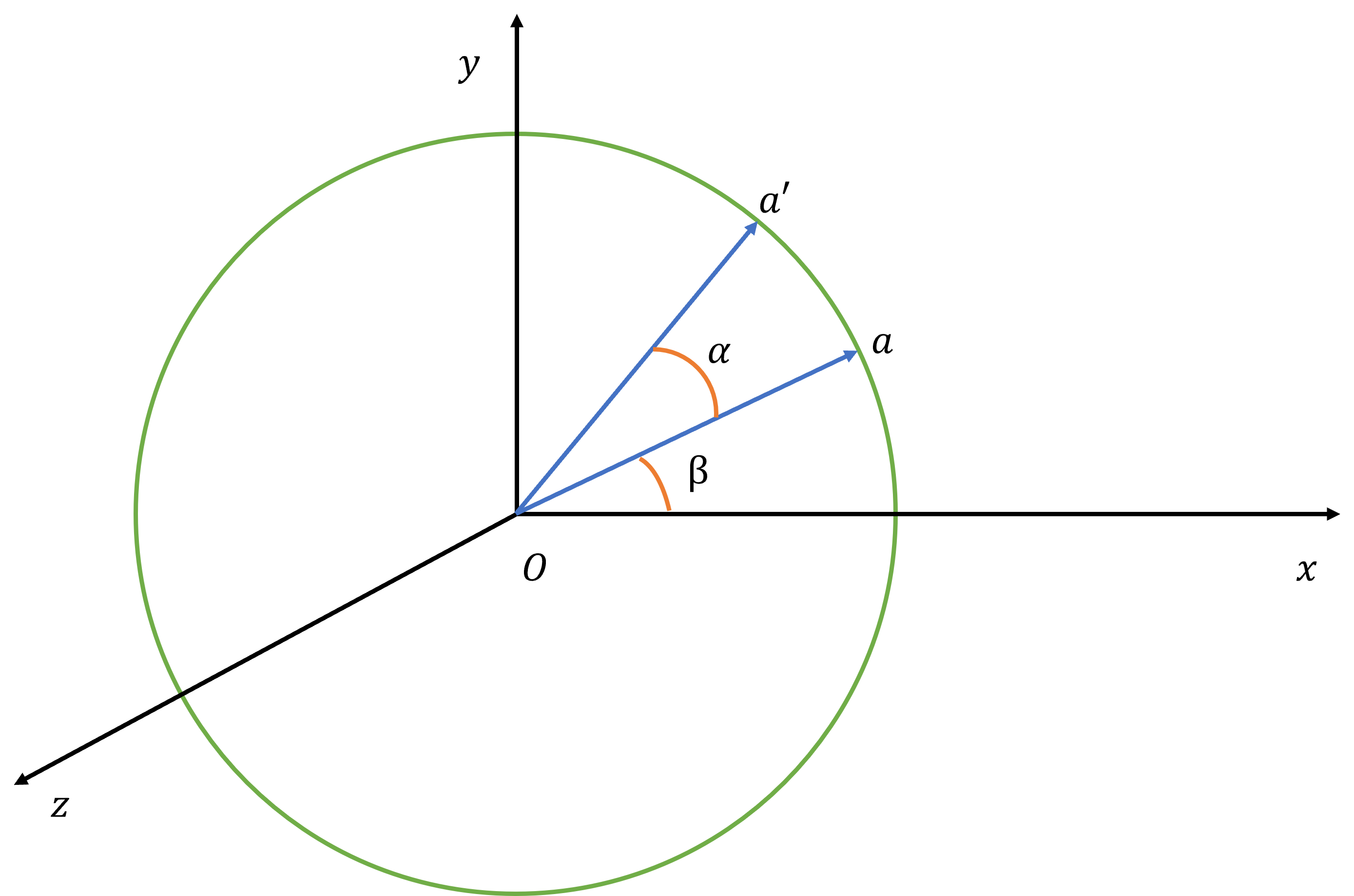
如上图所示,点\(a\)绕z轴逆时针旋转\(\alpha\)变为新的点\(a'\)。不妨设点\(a\)距离原点为\(\rho\),那么原始点\(a\)的坐标如下:
\[\begin{aligned}
x & = \rho \cos \beta \\
y & = \rho \sin \beta \\
z & = z
\end{aligned}
\]
旋转后的点\(a'\)的坐标为:
\[\begin{aligned}
x & = \rho \cos (\alpha + \beta) = \rho \cos \alpha \cos \beta - \rho \sin \alpha \sin \beta = x \cos \alpha - y \sin \alpha \\
y & = \rho \sin (\alpha + \beta) = \rho \sin \alpha \cos \beta + \rho \cos \alpha \sin \beta = x \sin \alpha + y \cos \alpha \\
z & = z
\end{aligned}
\]
因此绕y轴逆时针旋转\(\alpha\)的变换矩阵为:
\[P = \left[
\begin{matrix}
\cos \alpha & -\sin \alpha & 0 & 0 \\
\sin \alpha & \cos \alpha & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1
\end{matrix}
\right].
\]
矩阵的组合
使用矩阵进行变换的真正力量在于,根据矩阵之间的乘法,我们可以把多个变换组合到一个矩阵中。让我们看看我们是否能生成一个变换矩阵,让它组合多个变换。假设我们有一个顶点\((x, y, z)\),我们希望将其缩放2倍,然后位移\((1, 2, 3)\)个单位。我们需要一个位移和缩放矩阵来完成这些变换。结果的变换矩阵看起来像这样:
\[P_{Trans.Scale} = \left[
\begin{matrix}
1 & 0 & 0 & 1 \\
0 & 1 & 0 & 2 \\
0 & 0 & 1 & 3 \\
0 & 0 & 0 & 1
\end{matrix}
\right] \times \left[
\begin{matrix}
2 & 0 & 0 & 0 \\
0 & 2 & 0 & 0 \\
0 & 0 & 0 & 2 \\
0 & 0 & 0 & 1
\end{matrix}
\right] = \left[
\begin{matrix}
2 & 0 & 0 & 1 \\
0 & 2 & 0 & 2 \\
0 & 0 & 2 & 3 \\
0 & 0 & 0 & 1
\end{matrix}
\right].
\]
注意,当矩阵相乘时我们先写位移再写缩放变换的。矩阵乘法是不遵守交换律的,这意味着它们的顺序很重要。当矩阵相乘时,在最右边的矩阵是第一个与向量相乘的,所以你应该从右向左读这个乘法。建议您在组合矩阵时,先进行缩放操作,然后是旋转,最后才是位移,否则它们会(消极地)互相影响。比如,如果你先位移再缩放,位移的向量也会同样被缩放(译注:比如向某方向移动2米,2米也许会被缩放成1米)!